PART15Combination Logic Circuit

Experiment 2 :Encoder

Theory

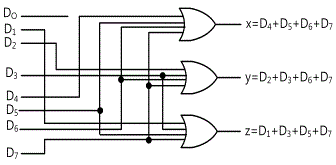
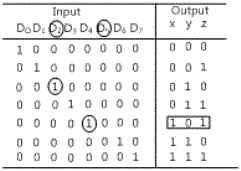
Encoder is the digital function that executes the inverse operation of decoder. The encoder has inputs of 2ⁿ and under and n outputs. Fig.15-4 is an example of the encoder. The octal-binary encoder needs 8 inputs because 8 digits need separate inputs, and 3 outputs to calculate corresponding binary number That is, the encoder is an encoding device. In the figure, the encoder is composed of OR gates whose inputs are determined from the truth table in fig.15-5. The output z becomes “1” when the input octal digit is odd number. The output y becomes “1” when the input octal digit is 2, 3, 6, 7. And the output x becomes “1” when the input octal digit is 4, 5, 6, 7. D₀ is not connected to any OR gates, and this is because the binary output should all become “0” in this case. However, when all inputs are “0”, the outputs all become “0”. This contradiction is solved by providing one additional output in order to indicate that all inputs are not “0”.

The encoder in fig.15-3 is supposed as only one input can become “1” in case of random situation. Otherwise, the circuit is meaningless. The circuit has 8 inputs. Therefore, 2⁸=256 input combinations are possible but only 8 among them have meanings.

The encoders determine the input priority and decode the input line that has the highest priority. Let’s say that in fig.15-4, the input that has higher subscript has higher priority than that has lower subscript. If D₂ and D₅ become “1” at the same time, the output will become [101] since D₅ has higher priority than D₂.

Experiment Process

1. The circuit on the left of Circuit-2 of M-15 means 4 to 2 encoder. Use the switch to change the input 0, 1, 2, 3 as in table 15-3 and measure the output A, B and record as 1 and 0 in the relevant column. (Check out the lighting of LED.)

2. The circuit on the right of Circuit-2 of M-15 means 10 to 4 encoder. As in table 15-4, measure the output A, B, C, D according to the input 1, 2, 3, 4, 5, 6, 7, 8, 9 and record the result in the relevant column. In fig.15-4, X means Don’t Care. Note that the inverter is attached to the output terminal.

tab1 print